Previously we talked in depth about the cutter speed but not a lot about the power or force. At the next meeting we had a lively discussion about whether changing direction would increase the life of the bull gear and pinion or decrease its life. In a room with 70 home shop machinists a few believed you could increase gear life by running in reverse (using the previously unused side of the gear), a few believed you decrease gear life (stressing the gear in a new way after it has been stress relieved in use for many years), but 90 percent of the members thought you would never see any difference or failure because the run time on a shaper by a home shop machinist is so small compared to the long life expectancy of the machine.

Dave Piper however brought an interesting perspective to the question by doing a little engineering work on the problem of force. The forward stroke is the power stroke and slow. The return stroke is fast with no load. Obviously the force on the gear teeth is at maximum in the middle of the power stroke. In the entire return stroke (and certainly in the middle) it would be minimum. If you reversed the motor then the maximum force would be in the middle of what used to be the return stroke.

What would be the maximum force applied on the teeth if the only change was to reverse the motor - that is if you kept the depth of cut and table feed the same?

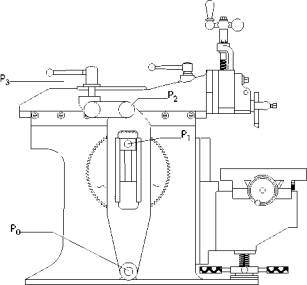
If point P₁ was not offset much (a short) stroke or if the length of the rocking arm (from P₀ to P₂) was very long with the bull gear very high (close to P₂) then the difference in force between forward and reverse would be negligible. Dave supplied some formulas so we can check the difference for some real numbers.

F = Cutting force.

F_G = Force exerted on the arm by the gear.

F_G1 = Force when offset is at top of bull gear (as pictured).

F_G2 = Force when offset is at bottom of bull gear.

T = Gear torque.

R = Radius of offset adjustment in bull gear.

X = Distance from P₀ to P₁.

X₁ = X when offset is at top of bull gear (as pictured)

X₂ = X when offset is at bottom of bull gear.

L = Length from P₀ to P₂.

The sum of the moments equals zero.

Our assumption is that the shaper and all its various components are moving relatively slowly. The cutting loads are continuous and constant and the dynamic loads are insignificant compared to the steady state cutting loads.

If this were not the case, then the above equation would not equal zero and we would have to factor in component weights, variation in load, spring when entering or exiting the cut, and etc. The dynamic load is relatively small and the cut relatively steady.

So imagine we are taking a "snap-shot" in time. We are looking at the instantaneous position when the ram is at mid stroke and the block, at P₁, is all the way up and/or all the way down. At this instant, the loads just balance each other and we can look at the problem as a static problem, not dynamic.

F_G2X₂ – F L = 0

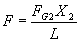
Transposing I get:

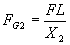
And therefore also:

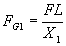
This says that F is constant and the force (F_G1 & F_G2) is proportional to X/L. This is the force at the sliding block not the force actually on the gear but what we care about now is just how much the force changes if we reverse the motor. For instance if it changes 39 percent (and it does) then the force applied to the gear would also be 39 percent higher if you reversed the motor.

Plug in values for L, X₁, X₂, and F and see the torque on the gear is T = F_G R.

Therefore the torque is proportional to the force F_G. Gear stress is proportional to F_G (assuming Hertzian contact stress).

For my 7” Rhodes these values are:

L = 16.5”

X₁ = 11.625”

X₂ = 8.375”

I don't know how to measure or properly estimate force F but all we care about is its relative change reflected back to F_G1 and F_g2. So I will assign a value to F of 50 pounds of force. This in turn would be a cut of something on the order of .025 deep x .005 wide in mild steel.

To calculate for force with a forward motor we would use values for X₁.

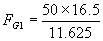
pounds.

The force with a backward motor direction would be calculated using X₂.

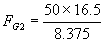
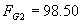pounds

So as you can see if you reverse the direction of the motor the force applied back on the gear increases substantially.

Keep sending email with questions and interesting shaper stories.

My email address is KayPatFisher@gmail.com.